Overtoner
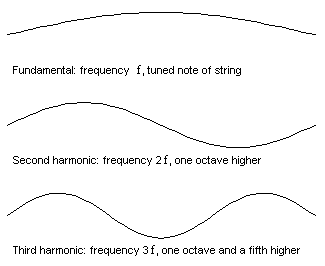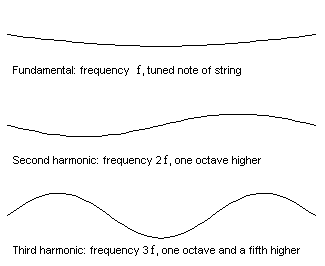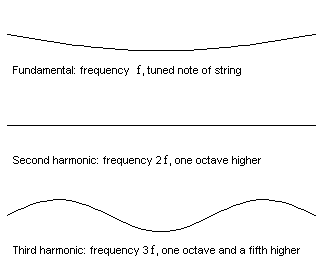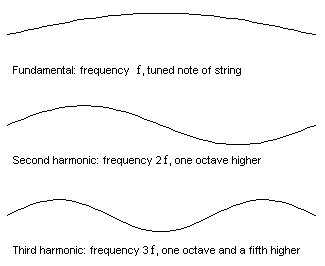
Overtoner fremkommer naturligt når man deler en streng eller når man blæser i en trompet uden ventiler. I animationen til venstre kan du se hvordan en streng kan svinge på tre forskellige måder med den dobbelte og 3 gange frekvensen. Strengen kan også svinge med 4, 5 6, 7... osv. gange. Det kaldes harmoniske overtoner. Det samme sker med luftsøjlen i en fløjte eller i en trompet. Den berømte franske matematiker Fourier viste at alle periodiske svingninger der er periodiske kan opdeles i et antal sinus kurver, der er harmoniske af grundperioden. Dvs. at alle toner der ikke er rent sinus formede, indeholder overtoner der er hele multiple af grundtonen.
Strengen på den nederste animation svinger som summen af de 3 bevægelser. Vi kalder den øverste grundsvingningen. Den næste for 2. harmoniske, den har den dobbelte frekvens af den øverste. Den 3. for 3. harmoniske med 3 gange grundfrekvensen.
Når man spiller på norsk sælgefløjte, eller på jagthorn uden ventiler, kan man kun spille naturtoner. Det vil sige at man ved at blæse på en bestemt måde kun rammer en ganske bestemt overtone, (og denne overtones overtoner.)
De laveste toner på sådan et instrument ligger langt fra hinanden, men når man kommer længere op, ligger tonerne tættere.
Klokker og metal stænger der laver overtoner, der som regelen ikke harmoniske med grundtonen.
Med fourrier analyse kan man vise at en kurve der er firkantet kun giver ulige harmoniske. (dvs. 1.3.5.7 osv. harmoniske) medens en kurve der er formet som en savtak, giver lige harmoniske dvs. 1.2.4.6.8 osv. gange grundtonen) . Det menneskelige øre er vældigt godt til at genkende harmoniske familier.
Øret kan genkende grundtonen, selv om man har filtreret den fra. Derfor kan man godt fornemme bassen, selv om man hører på en dårlig radio hvor bassen ligger udenfor det frekvensområde som radioen kan gengive. Det kan vises at lyden fra de dybeste strenge på et klaver i nogen tilfælde er så svage at de ikke kan høres, når man alligevel hører tonen, er det fordi at overtonerne kan høres, og øret gætter sig til grundtonen.
To toner klinger godt sammen når deres overtonerne mødes. Ved eksperimeter med strenge instrumenter fandt grækerne ud af, at intervaller hvor to strenge stod i forhold 2/1, 3/2, 4/3, 5/4, 6/5,7/6,8/7,9/8,10/9 og så videre klingede specielt godt sammen. Man kalder disse talforhold (1+n)/n eller epimoriske talforhold. Selvom Grækerne ikke lykkedes at definiere begrepet frekvens, men målts strengenes længdeforhold, er de talforhold de beskriver frekvensforholdet mellem tonerne.
Det skyldes at de fortrindsvis brugte harpelignende instrumenter (Lyra og Khithara) uden gripebrædt, og de startede at regne deres skala (eller tonoi) fra oven og nedefter. Derfor er de talforhold de beskriver svarende til frekvensforhold. Hvis vi skal udtrykke frekvensforholdene som længde forhold på en violin streng, vil man få det omvendte forhold.
Jo lavere tal i det epimoriske talforhold, desto bedre klinger strengene sammen.
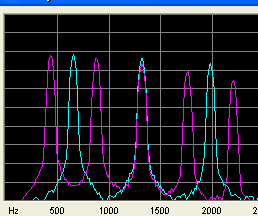
Frekvens spektrum af de første 5 harmoniske af tonen A 440,0 Hz og E 660,0 Hz Det ses at den anden harmoniske af 660 Hz mødes med den tredie harmoniske fra A-et.