Svævninger
Når to toner mødes og der er en meget lille frekvensforskel mellem dem opstår der svævninger. Det er ligesom tonen siger whoh-whoh-whoh-whoh-whoh-whoh. Svævningerne har en frekvens der svarer til forskellen på de to frekvensen af de to toner..
Klik her og du kan du høre tonerne 659.26 Hz og 660.00 Hz. (Det tempererede og det rene E sat sammen) Der kan tydelig høres en 4 svævninger på de 6 sekunder tonen varer svarende til at der 0.74 Hz forskel mellem tonerne.
Hvad er svævninger
Svævninger opstår fordi den bølge der er svinger hurtigere "overhaler" den langsomere. Frekvensen som dette sker med svarer til forskellen frevensen af de to toner.
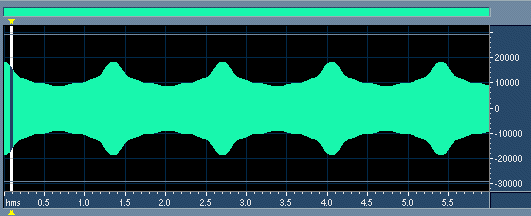
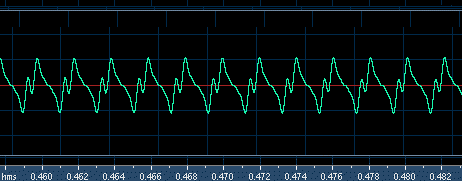
På billedet ovenfor kan du se hvordan de seks sekunders svævning ser ud man kan ikke se den enkelte svingning, men man kan se svævningen. Nedenunder er taget et lille (10 millisekunders) udsnit af de 6 sekunder for oven, og kan du lave en animation ved at klikke. (Animationen er ikke koblet sammen med lyden desværre) Klik på langsommere for at køre halvt så hurtigt. (du kan klikke flere gange på langsommere - du kan også køre "filmen" som enkeltbilleder.
Start animation | Langsommere | Langsomt | Hurtigt | Enkeltstep | Hør tonerne
På billedet ser du hvordan svævninger opstår i en når to lydbølger med forskellige bølge længde mødes. Når den lille bølge "indhenter" den store, vil de to bølger forstærke hinanden og den samlede bølge højde som er summen af de to bølger vil være større, det vil sige at lyden bliver kraftigere. Når de to bølger er hver for sig, vil den bølge højden være lavere. Når man hører to svingninger hvor frekvensen er meget tæt på hinanden vil man høre svævninger der svarer til forskellen på de to frekvenser. I ovenstående billede har den lille bølge frekvensen 660Hz, mens den store har 659.26 Hz. Fænomenet gentager sig med forskellen som er 0.74 Hz. Det vil sige 4½ gange i eksemplet, der varer 6 sekunder.(Det er muligt at du kan høre det dobbelte, men det skyldes at jeg har lavet tonen med 2.3.4. og 5. harmoniske, og at disse specielt 2 harmoniske også interfererer og laver svævninger.)
Undertoner
Svævningen kan også udregnes fra den så kaldte logaritmiske cosinus formel:
| cos(x) + cos(y) = 2 cos | ( | x + y 2 |
) | cos | ( | x – y 2 |
) |
Man ser her at for to forskellige frekvenser x og å vil der opstå et bidrag fra middelfrekvensen (x+y)/2 og den halve difference frekvens (x-y)/2
Hvis afstanden mellem tonerne er større end en halv tone, vil man kunne høre en "undertone" svarende til difference frekvensen mellem de to toner. Hvis de 2 frekvenser er epimoriske det vil sige af formen 2/1 3/2 4/3 5/4 6/5 ... (n+1)/n vil undertonen være harmonisk i forhold til de to toner. Dessuden sørger forholdet for at det harmoniske blander sig pænt og mødes. I oldtidens grækenland gik man meget op i de epimoriske intervaller. Man havde et navn for hvert af dem
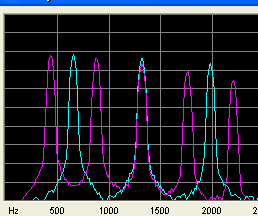
Her ser du frekvensanalysen af et Rent A=440Hz og et Rent E=660Hz.
Ud over det faktum at de harmoniske falder sammen på 3*440=2*660=1320Hz
så vil du også se at det samlede spektrum ligner meget et spektrum af
de harmoniske tonen 220Hz Denne tone er der ikke. Øret virker sådan, at
når det møder en harmonisk tone-række, uden grundtone, så vil det selv
"digte en grundtone" Derfor vil man kunne høre det lave A når man stemmer
A og D-strengen sammen. Dette er en spøgelsestone, der ikke er der.
Spektret indeholder 2. 3. 4. 6. 8. og 9 harmoniske af 220 Hz. Læg mærke til at 5. og 7. harmoniske af undertonen mangler.