Den diatoniske (harmoniske) skala
Den harmoniske skala kaldes også "Just intonation" på engelsk. (Den skal ikke forveksles med harmonisk mol, som er et andet begreb )
Hvis du sætter fingeren ned på den halve (1/2) streng får du en oktav.
Sætter du fingeren ned på 1/3 af strengen (sådan at der er 2/3 dele tilbage) får du en ren kvint
Sætter du fingern ned på 1/4 af stremgen (sådan at der er 3/4 tillbage) får man en ren kvart
Sætter du fingern ned på 1/5 af strengen (sådan at der er 4/5 tillbage) får en ren stor terts.
Sætter du fingern ned på 1/6 af strengen (sådan at der er 5/6 tillbage) får en ren lille terts.
Grunden til at ovenstående intervaller lyder godt, er at når man spiller dem sammen med grundtonen, så mødes overtonerne, og det kan det menneskelige øre godt lide.
Hvis man tager strenge og stemte efter grundtonen, 1/5, 1/3 og 1/2 af strengen. efter ovenstående skema, og han fik den smukke klang som vi idag på dansk kalder treklang.
Hvis vi tager grundtonen plus 1/6, 1/3 og 1/2 får vi en mol akkord.
Hvis man tager alle tonerne som vi nu har lavet vil vi finde ud af at vi har 7 toner. Dem kalder vi en skala. I skalaen ligger nogen toner tættere end andre. For eksempel ligger tertsen tæt på kvarten. Vi kalder tonerspringet mellem disse for et halvt tonerspring.
Man kunne jo også udgå fra kvinten og lave en treklang, det er det vi kalder for dominanten.
Hvis man tager alle tonerne som vi nu har lavet vil vi finde ud af at vi har 7 toner. Dem kalder vi en skala. I skalan ligger nogen toner tættere end andre. For eksempel ligger tertsen tæt på kvarten. Vi kalder tonespringet mellem disse for et halvt tonespring.
Matematisk finder vi de mellemliggende toner ved at gange frekvenserne.
Det gode ved denne skala er, at den lyder utroligt godt. Men ligesom Pythagoras skala har den en mangel, hvis man bevæger sig harmonisk langt væk fra udgangspunktet. (Dvs. man tager treklange på andre toner i skalaen) så går det galt. Den har også en anden mangel: Tonerne flytter sig afhængigt af hvad man skal harmonisere med. Det vil sige at i princippet er det svært at spille mere end 2-stemmighed.
Man kan regne intervallerne ud ved at gange. Den store sekund fremkommer ved at man tager strengelænden for kvinten og ganger med sig selv 2/3*2/3 = 4/9 og gange med 2 (for at komme en oktav ned)
(Regnestykket kan også gøres med frekvensernes forhold 3/2 * 3/2 = 9/4 Her skal man så dividere med 2 for at komme "hjem".
Den diatoniske skala kan altså skrives:
| Interval navn | Prim | Stor Sekund | Stor Terts | Kvart | Kvint | Stor Sekst | Stor Septim (ledetone) | Oktav |
| Tone trin | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Udledes af | Grund-tonen | Kvint + kvint | stor terts | kvart | kvint | stor terts + kvarten | stor terts +kvinten | kvartens kvint |
| Fingerns position | Hele strengen | 1/9 | 1/5 | 1/4 | 1/3 | 2/5 | 7/15 | 1/2 |
| Resterende streng | 1 | 8/9 | 4/5 | 3/4 | 2/3 | 3/5 | 8/15 | 1/2 |
| Frekvens forhold | 1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 1/2 |
|
Frekvens forhold til forrige tone |
9/8 | 10/9 | 16/15 | 9/8 | 10/9 | 9/8 | 16/15 | |
| Tone i A-dur |
440 | 495 | 550 | 586.666 | 660 | 733.33 | 825 | 880 |
Med MS IE kan du høre tonerne når du fører musen henover dem. Med lidt øvelse kan du lave intervaller etc. Læg mærke til at dette er rene toner, ikke de sedvanlige tempererede toner.
Nu kunne man også starte et andet sted i skalaen. For eksempel på kvinten, kvarten. Man kunne også bruge de samme toner og starte på sekund, eller sekst. På Phytagoras tid var der forskellige folkeslag der brugte de forskellige skalaer, og han opkaldte dem efter dem. Da Gregorius den store indførte den Gregorianske sang på 400-tallet, brugte han de navne på skalaerne som Phytagoras havde givet dem, han kom godtnok til at bytte rundt på dem, men det er de Gregorianske navne, der gælder nu. Sjovt nok brugte Gregorius hverken vores Dur eller Mol, de kom vistnok først til i middelalderen.
Matematik og intervaller
I tabellen ovenfor indgår en masse talforhold. Det nemmeste er nok at regne i frekvenser.
Når du fordobler frekvensen kommer du en oktav op.
Hvis du skal gå en kvint op skal du gange din frekvens med 1 divideret med strengelængden af den resterende streng.
Dvs:
Kvint 3/2
Kvart: 4/3
Stor terts 5/4
Lille terts 6/5
Hvis du lægger 2 intervaller sammen, skal du gange frekvensforholdene: Sekst = 4/3*5/4=(4*5)/(3*4) =5/3
(idet man ganger en brøk ved at gange tæller og nævner sammen)
Det ser jo meget godt ud, men kan man altid gøre det? og går det altid godt.
Nej det kan man ikke!!!
Nedstående eksempel blev opdaget af Didimos en musikteoretiker der levede i Alexandria århunderet f. Kr.
Du kan nemt gentage det på din violin.
Det didymiske komma
Stem din violin helt rent. Så spiller du første finger (H) sammen med D-strengen og lytter efter at det lyder rigtigt godt. Så spiller du H sammen med E-strengen. Hvad søren... for at få det til at lyde godt skal du flytte fingeren 4 millimeter længere op!
Det skyldes at når du intonerer sammen med D-Strengen, laver du en naturligt ren sekst. som jo er en stor terts under oktaven til D-strengen. Når du spiller sammen med E-strengen laver du en ren kvart under E-strengen. Men E-strengen er jo stemt 2 rene kvinter over D-strengen.
For at gå fra D-strengen til E-strengen ganger vi frekvensen med 9/4 For at gå herfra ned til tonen H skal vi dividere med 4/3. For at gå fra D til H direkte skal vi gange frekvensen med 3/5.
Sætter vi de to frekvenser i forhold til hindanden får man (9/4)/(4/3) * 3/5 eller (9*3*3)/(4*4*5)
Dvs. frekvensen er 81/80 højere. eller forskellen i strengens længde er 80/81 Da en violin streng er 330 mm. skal man flytte fingeren ca. 4 millimeter eller et 1/8 tonetrin.
Konklutionen er at selv om den harmoniske intonation lyder smukkere, fordi at intervallerne er rene, så opstår der nogle modsætninger hvor talforholdene ikke går op, og hvor akkorderne ikke bliver rene. Eller rettere, der er flere muligheder for at spille den samme tone rent afhængigt hvad man sammenligner med.
I dette eksempel har vi en kvart fra E-strengen til H og en sekst fra D-strengen til H. E- og D streng er stemt som 2 rene kvinter.
Problemet er ikke så stort når man spiller 2 violiner sammen. Her kan man faktiskt spille renstemt, og det lyder smukkere end hvis man spiller tempereret.
Men hvis der er en guitar med, bliver man nærmest nødt til at spille tempereret i stedet for ren stemt. (se næste)
Se også den pythagoræiske skala
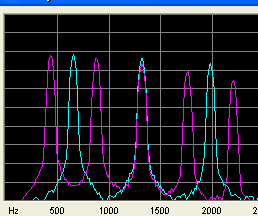
Billedet viser frekvens analys af en tone og sin kvint. Som man kan se falder den anden harmoniske af kvinten sammen med den 3 harmoniske af grundtonen. Dette gentager sig for den 6 harmoniske og den4 harmniske af kvinten osv. (ikke med på billedet)
Det er formentlig dette sammenfald af overtoner der gør at vi føler harmoni.
For kvarten sker sammenfaldet på den 4. harmoniske af grundtonen, der sammenfalder med den 3. harmoniske af kvarten.
For den store og den lille terts sker sammenfaldet endnu højere oppe.
Det er interessant at notere at tonespringene imellem de forskellige toner er ikke ens. F.eks. er heltonen op til sekunden
Den harmoniske skala har to forskellige heltoner 9/8 (frekvensforhold prim-sekund og kvart-kvint) og 10/9 (mellem Kvint og sekst)