Övertoner
Övertoner framkommer naturligt när man delar en sträng eller när man blåser i en trumpet utan ventiler.
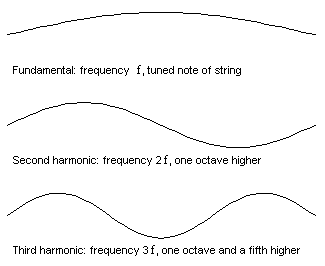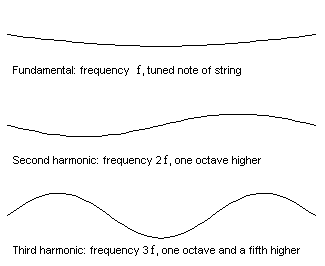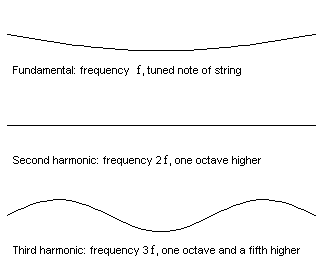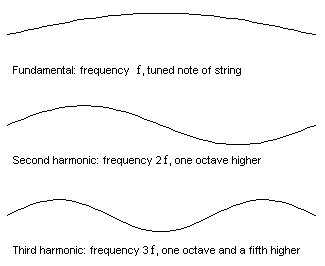
På animationen till vänster kan du se hur en sträng kan svänga på olika sätt med dubbla och tre gånger grundfrekvensen. (Strängen kan också vibrera med 4,5,6,7 o.s.v. gånger grundfrekvensen. Det kallas harmoniska övertoner.
Det är likadant med luftpelaren i en föjt eller i en trumpet. Den berömda franska matematikern Fourier visade att alla periodiska svänginger kan updelas i ett antal sinus kurvor, som är harmoniska med grundperioden. Med andra ord alla toner som inte är rent sinusformade innehåller övertoner.
Strängen på den nedersta animationen svänger som summan utav dom 3 rörelserna. Vi kallar den översta för grundsvägningen, den nästa för den andra harmoniska, den 3dje för den 3dje harmoniska.
Om man spelar på säljfläjt, eller jathorn utan ventiler, kan man enbart spela naturtoner.
De lägsta tonerna på et sådant instrument ligger lång från varnadra, men när man kommer längre upp, ligger tonerna tätare.
Klockor och metal stänger producerar övertoner som inte är harmoniska med grundtonen. Detta är för att de olika svängningsmönstrena i fasta föremål är mycket mera komplicerade en i et luftrör eller en sträng.
Det mänskliga örat är väldigt bra på at känna igen harmoniska serier.
Örat kan känna igen grundtonen, även om man har filtrerat bort den! T.ex. kan man höra basen på en dålig radio, även om radion inte kan producera den frekvens som basen ligger på. Det är för att örat hör basens övertoner, och utifrån avståndet på övertonerna "gissar" örat var grundtonen ligger.
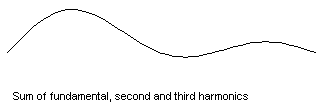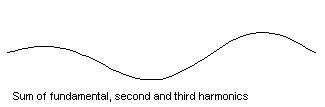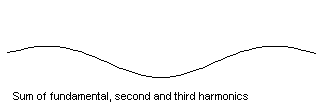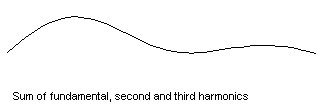
Två toner klingar bra ihop när övertonerna möts. Genom at experimentera med olika stränglängder kom grekerna i antiken på at stränglängder med talförhållandena 2/1, 3/2, 4/3, 5/4, 6/5,7/6,8/7,9/8,10/9 klingar bra ihop Man kallar dessa talförhållande (1+n)/n eller epimoriske talforhold. Trots at antikens greker inte lyckades at definiera begreppet frekvens,
Selvom Grækerne ikke lykkedes at definiere begrepet frekvens, men målts strengenes længdeforhold, er de talforhold de beskriver frekvensforholdet mellem tonerne.
Grekerna använde harpa-liknande instrument (Lyra och Khithara), som inte hade greppbräda, och de startade att räkna deras skala eller tonoi uppifrån. Därför stämmer de talförhållande, som de beskriver överens med frekvensförhållanden. När vi förkortar strängen med fingrar på en fiol, räknar vi intervallet nerifrån och uppefter. Vi skall därför anvfända det inversa talförhållandet i förhållande till frekvens förhållandet. (2/1, 2/3, 3/4; 4/5 6/5 osv)
Ju lägre tal i det epimoriska förhållandet, desto bättre harmoni. Sålunda klingar oktaven bättre ihop än kvinten, och kvinten bättre än kvarten.
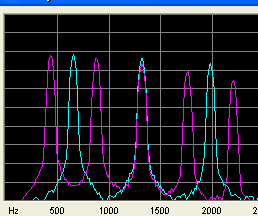
Frekvens spektrum av de första 5 harmoniske af tonen A 440,0 Hz og E 660,0 Hz Det framtår att den andra harmoniska komponenten af 660 Hz møts med den tredje harmoniska från A-et.